
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ НЕУСТАНОВИВШЕГОСЯ ДВИЖЕНИЯ ВОДЫ
В настоящее время большинство исследователей в качестве мате-матической модели описания процесса неустановившегося плавно изме-няющегося движения воды в открытых руслах используют дифференциальные уравнения Сен-Веиана. Существует много различных форм записи этих уравнений. Р. Р. Чугаев приводит их в таком виде:

1) уравнение неразрывности (баланса расхода)
2) уравнение динамического равновесия
В левой части уравнения (18-2) величина i — является уклоном свободной поверхности воды. Первый член в правой части уравнения (18-2) представляет собой уклон трения; второй член изменение кинетической энергии по длине; третий член dt— локальную часть сил инерции.
Уравнения (18-1) и (18-2) являются неполной моделью неустановившегося движения открытых потоков. Здесь не учитывается поверхностное натяжение, кривизна струй, вертикальная составляющая ускорений и ряд других факторов. Однако эта модель при анализе волнового движения для практических целей вполне удовлетворительна. Дифференциальные уравнения (18-1) и (18-2) гиперболического типа решить в квадратурах невозможно. Поэтому предложено много методов приближенного решения этих уравнений, основанных на тех или иных допущениях.
При исследовании неустановившегося режима граничные условия для верхнего створа (в НБ у здания ГЭС) обычно задаются графиком изменения мощности- ГЭС N (t) или ее расхода Q(t). Для нижнего, удаленного от ГЭС створа граничные условия определяются кривой связи расходов Q и уровнем воды Z в условиях установившегося режима Q(Z).
При исследовании неустановившегося режима в подводящем канале ГЭС граничные условия задают для верхнего створа в виде Q(Z) или Z= const. Для нижнего створа (у напорного бассейна) гра- :ничными условиями считают график изменения мощности ГЭС N(t) или ее расхода Q(t).
Начальным условием обычно считают установившийся режим движения воды.
Суточное регулирование расходов .ГЭС и ГАЭС представляет собой периодический процесс, и силы инерции при неустаиовившемся режиме в бьефах и каналах оказывают заметное влияние на колебания уровней воды.
Решение уравнений неустановившегося движения производится с использованием ЭВМ. В гироэнергетических расчетах наибольшее рас-пространение получают способы расчета, основанные на подробном математическом моделировании происходящего процесса. .К таким моделям можно отнести систему уравнений в частных производных Сен-Венана (одномерная модель).
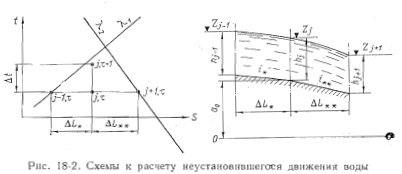
Уравнения Сен-Венана не имеют аналитического решения в квадратурах. Поэтому для их интегрирования используются различные приближенные методы. Наибольшее распространение получили два метода решений — явный и неявный методы конечных разностей.
Явный метод конечных разностей достаточно прост в вычислительном плане и имеет хорошую устойчивость при решении уравнений (18-2) при явно выраженном неустаиовившемся движении воды, для которого справедливы уравнения (18-2). Однако он обладает существенным недостатком — шаг интегрирования по времени жестко ограничен условием сходимости данной схемы к точному решению. Этот метод широко применяется для расчетов переходных процессов в деривационных каналах гидроэнергетических установок. . Как правило, эти каналы имеют длину, не превышающую несколько километров. Поэтому в них наблюдается наложение (интерференция) волн при суточном регулировании. Период колебательных процессов оказывается соизме-рим с допустимым шагом по времени в явной разностной схеме.
Неявный метод решения уравнений Сен-Венана более громоздкий в вычислительном плане, зато позволяет снять ограничение по шагу интегрирования во времени. Это обстоятельство чрезвычайно важно при расчетах прохождения паводков и попусков в открытых руслахбольшой длины. Здесь процесс прохождения неустановившегося движения воды длится недели, а то и месяцы. Провести расчеты такого режима по явному методу оказывается очень сложно из-за малого шага во времени.
Таким образом, при небольшой длине открытого русла или канала и коротком периоде, для которого необходимо получить характеристики переходного процесса, целесообразно использовать для уравнений Сен-Венана явный метод конечных разностей, а при продолжительном переходном процессе в длинных руслах — неявный метод.
Для энергетических каналов запишем систему уравнений (18-1) и (18-2) в таком виде:

Вычисления на ЭВМ можно осуществить по схеме, которая представлена на рис. 18-3.
