
ФИЗИЧЕСКАЯ СУЩНОСТЬ ПРОЦЕССА РАБОТЫ ГИДРОЭЛЕВАТОРА И ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАСЧЕТА ГИДРОЭЛЕВАТОРОВ
Струя воды, вылетающая из насадка, попадает в горловину (рис. 81, а). В начальный момент работы, когда пространство А, представляющее собой объем приемной камеры, заполнено воздухом, струя воды будет увлекать этот воздух в горловину. Интенсивность увлечения будет зависеть от состояния поверхности струи, которая, в свою очередь, обусловливается скоростью струи. Если скорость очень велика, то на поверхности струи образуются завихрения, увлекаемые струей, причем это поступательное движение сопровождается вращением конечных масс диспергированной на поверхности струи жидкости. Воздух интенсивно увлекается вихрями и поступает в камеру смешения. Если скорость струи невелика и не наблюдается вихревых масс вокруг струи, то поверхность струи может быть волнистой или гладкой (ровной). Волнистая поверхность обеспечивает более интенсивное увлечение воздуха, так как волны дополняют некоторые порции воздуха к увлекаемому трением в результате поршневого действия волн при их касании внутренней поверхности горловины (рис. 81,б).
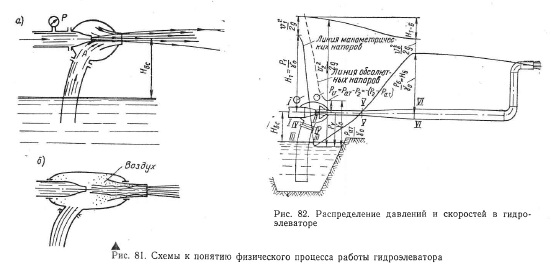
Сущность процессов, происходящих в потоке, можно описать уравнением Бернулли для участка системы между сечениями I—I и II— II (рис. 82):

Сечение взято перед насадком гидроэлеватора, а сечение II—II совпадает с выходным отверстием. Потери напора в насадке h можно определить по формуле местных потерь:
Величина корректирующих коэффициентов — коэффициентов Кориолиса — не превышает 1,1 и обычно в задачах, подобных гидравлическому расчету гидроэлеватора, принимается равной единице.
Давление перед насадком обычно известно. Оно равно давлению, развиваемому насосом, который обслуживает гидроэлеватор, за вычетом потерь напора в подводящем трубопроводе. Следовательно, абсолютное давление р2 в приемной камере однозначно определяется из уравнения (133). В данном случае ось гидроэлеватора принята горизонтальной; при условии, что ось будет наклонной, затруднений в решении задачи не возникает.
Теперь рассмотрим движение жидкости на участке трубы между сечениями III—III и IV—IV, т. е. от поверхности жидкости в водоеме (или зумпфе) до конца всасывающей трубы—до приемной камеры, давление в которой уже известно из решения уравнения (133).
Уравнение Бернулли для участка между сечениями III—III и IV—IV, учитывая, что область входа жидкости во всасывающую трубу является местным сопротивлением для рассматриваемого потока жидкости, будет иметь вид
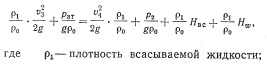
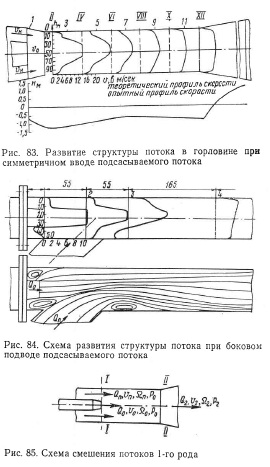
Скорость понижения уровня в водоемах как естественных, так и искусственных (зумпф или приемник) очень мала, поэтому членом можно пренебречь.
Значение рат принимается равным 1 кгс/см2 или берется по показанию барометра.
Всасывающая труба имеет обычно постоянный диаметр DBC. Скорость движения жидкости в ней называется скоростью всасывания, поэтому.
Всасывающая способность гидроэлеватора достаточно высокая, и высота всасывания Я вс допускается до 8 м (для чистой воды и гидросмесей незначительной консистенции).
При всасывании грунта потери Hw иногда трудно определить достаточно точно в связи со сложностью процесса отрыва грунта и вовлечения его во всасывающую трубу. В общем случае
При всасывании чистой воды расстояние от всасывающей трубы до дна водоприемника не должно быть менее 2,5 DBC.

Наиболее трудно охарактеризовать процесс смешения рабочего и всасываемого потоков жидкости в горловине гидроэлеватора и передачу энергии рабочего потока засасываемому.
В данном случае уравнение Бернулли неприемлемо, поскольку поток состоит как бы из двух потоков: рабочего, имеющего большую скорость, и увлекаемого им подсасываемого потока, имеющего меньшую среднюю скорость движения. Поток рабочей жидкости, очевидно, передает всю возможную энергию подсасываемому потоку тогда, когда произойдет полное смешение их, т. е. потоки рабочей и подсасываемой жидкости образуют один общий поток с типичным для однородного турбулентного потока распределением скоростей.
На рис. 83 приведены опытные данные, характеризующие развитие структуры потока в горловине при симметричном вводе в горловину подсасываемого потока. Из рисунка видно, что по мере продвижения жидкости в горловину поток становится однородным (т. е. перестают существовать раздельно рабочий и подсасываемый потоки). Длину камеры смешения (горловины) 1\ следует выбирать так, чтобы в конце ее поток имел нормальное распределение скоростей.

На рис. 84 приведены опытные данные Н. А. Маньжова, характеризующие развитие структуры потока в горловине при боковом вводе подсасываемого потока. Опыты показывают, что работа гидроэлеватора более эффективна при симметричном подводе подсасываемой жидкости в камеру смешения.
В настоящее время нет строгой теории работы гидроэлеватора, но имеется большое число экспериментальных исследований процесса всасывания жидкости гидроэлеватором. Особенно много исследований посвящено смешению потоков в горловине.
К потокам в насадке и во всасывающей трубе, а также в диффузоре и напорной линии, если к диффузору поток поступил вполне смешанным, применимо уравнение Бернулли, из которого находят необходимые параметры.
Для рассмотрения движущейся жидкости в горловине используют два решения: теорему о количестве движения или теорию турбулентного перемещения струй. Применимы оба решения, но получаемые теоретические данные требуют экспериментальной корректировки.
Первое решение задачи о смешении потоков в горловине гидроэлеватора, основанное на теореме о количестве движения, было дано Г. Цейнером. Применим эту теорему к массам жидкости, проходящим через сечения I—I и II—II (рис. 85), приняв промежуток времени равным 1 с, т. е.
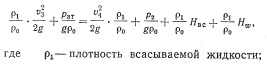

При составлении этого уравнения принято, что давления распределены по сечению равномерно, а также не учтены потери по длине смесительной камеры; АГ—1 с.
Ось гидроэлеватора горизонтальная, подсасываемый поток имеет то же направление, что и рабочий. Выражая массу как произведение
При одинаковых плотностях рабочей и подсасываемой жидкостей уравнение (135) приводится к виду:
Энергия потока после смешения, т. е. в сечении II—II, равна:
Потеря энергии на смешение потоков в горловине, т. е. между сечениями I—I и II—II, будет равна:
При боковом подсосе жидкости гидроэлеватором (под прямым углом) (рис. 86) потери энергии больше на величину в гидроэлеваторах следует предусматривать плавный подвод подсасываемой жидкости, т. е. под небольшим (острым) углом к оси гидроэлеватора.
Теория Цейнера не дает указаний к выбору длины камеры смешения, однако поперечные размеры могут быть приняты исходя из условий обеспечения наивыгоднейшего значения скорости v2, при котором будут наиме ньшие потери в камере смешения.
Для определения наивыгоднейшего з начения скорости v2 следует взять производную от выражения для потерь энергии (139) ьо скорости v2 и результат приравнять нулгэ, т. е.:
Энергия потока подсасываемой жидкости в том же сечении определится по формуле
Потери энергии в диффузоре этим уравнением не учитываются.
Исследования Цейнером были проведены очень давно. За истекшее время сделано большое число попыток усовершенствовать или уточнить и пополнить работу Цейнера, например исследование Л. Д. Бермана, использованное позднее Б. Э. Фридманом при составлении им инженерного метода расчета гидроэлеваторов. Л. Д. Берман внес ряд поправок в уравнения Цейнера, в частности принял, что минимум потерь в гидроэлеваторе определяется оптимальным значением v2. Принятые поправки и допущения не имеют универсальной достоверности, поэтому область применения решения Бермана и опирающегося на него решения Б. Э. Фридмана ограничена.
Результативным соотношением, вытекающим из исследований Л. Д. Бермана и доработок Б. Э. Фридмана, является равенство

Полученное соотношение (141) означает, что для гидроэлеваторов с наивыгоднейшими геометрическими размерами полный напор на обрезе насадка должен быть во столько раз больше напора, развиваемого гидроэлеватором за диффузором, во сколько раз площадь сечения цилиндрической камеры смешения больше площади выходного сечения насадка. Соотношение (141) и его расшифровку иногда принимают за основной элемент в методике инженерного расчета гидроэлеваторов, поэтому необходимо оговорить область применимости этого соотношения, опираясь на имеющиеся экспериментальные данные по исследованию работы гидроэлеваторов.
Соотношение (141) соответствует наибольшему значению к. п. д. гидроэлеватора при следующих конструктивных условиях и режиме работы гидроэлеватора:
камера смешения должна иметь цилиндрическую форму и длину, равную на которой смешиваемые потоки развивают нормальную структуру турбулентного потока, т. е. обеспечивают симметричную эпюру распределения локальных скоростей, удовлетворяющую логарифмическому закону;

расстояние от торца насадка до входного сечения горловины следует принимать равным
горловина должна иметь входную конфу- зорную, хорошо закругленную часть протяженностью примерно;
угол конусности диффузора должен быть около 8—10°;
необходимо, чтобы гидроэлеватор имел небольшую вакуумметрическую высоту всасывания (1 м вод. ст.).
Указанные условия, а также соотношение имеют ориентировочный характер и приближенное значение.
