
РАСПРЕДЕЛЕНИЕ ТВЕРДЫХ ЧАСТИЦ (ПО КОНСИСТЕНЦИИ) ПО СЕЧЕНИЮ ПОТОКА ГИДРОСМЕСИ
Распределение концентрации твердых частичек по сечению потока гидросмеси неразрывно связано с механизмом отрыва твердых частиц от дна потока и переноса их во взвешенном состоянии. Впервые теоретически этот вопрос, по-видимому, был поставлен французским ученым Дюпюи (1848 г.). Весь механизм подъема частиц в потоке Дюпюи объяснил разницей скоростей в толще потока. К этому своеобразному применению принципа Бернулли неоднократно возвращались ученые более поздних времен, причем следует признать, что этот принцип в механизме распределения твердых частиц в толще потока имеет действительно большое значение.
М. А. Великанов, анализируя теорию Дюпюи, признал, что эффект разницы скоростей над твердой частицей и под ней (именуемый иногда эффектом Магнуса) проявляется только в придонной области, где градиент скорости велик, т. е. может управлять механизмом отрыва частиц только от дна. В толще потока, где градиент скорости незначителен, как полагал М. А. Великанов, значение этого эффекта во взвешивании частиц невелико (необходимо отметить, что М. А. Великанов в основном изучал потоки малой мутности).
Наличие твердых частиц в потоках высокой консистенции изменяет эпюру скоростей по вертикалям в сечении потока. Большое значение градиента скорости сравнительно равномерно сохраняется от дна до кинематической оси потока, в результате чего создаются благоприятные условия для проявления эффекта Дюпюи — Магнуса почти во всей толще потока. Некоторое снижение этого эффекта от дна до кинематической оси происходит от того,, что при транспортировании разнородного грунта у дна движутся во взвеси более крупные частицы, а в верхних слоях — преимущественно мелкие.
Наличие в турбулентном потоке макрострук- турных (крупномасштабных) образований в виде вальцов обусловливает перемешивание жидкости в потоке; пульсация местных скоростей свидетельствует о переносе из слоя в слой малых объемов жидкости, что в совокупности с крупными вихрями создает полную картину так называемого турбулентного перемешивания в потоке.
Если поток переносит какое-либо вещество, взвешенное или растворенное в нем, или обладает тем или иным свойством (например, нагретостью), то все эти переносимые субстанции участвуют в какой-то мере в турбулентном перемешивании потока и в зависимости от интенсивности перемешивания и свойства переносимой субстанции соответственно распределяются по живому сечению потока.
Диффузионная теория взвешивания наносов
Основной диффузионной теории взвешенного переноса твердых частиц водными потоками является схема турбулентного перемешивания, согласно которой конечные массы жидкости в турбулентном потоке, постоянно перемешиваясь, поддерживают во взвешенном состоянии переносимые твердые частицы, причем на место поднимающихся снизу вверх масс жидкости, более насыщенных твердыми частицами, устремляются сверху вниз равные по объему количества жидкости, но менее насыщенные твердой составляющей.
Основоположником этой теории является В. Шмидт. Уравнение Шмидта для переноса невесомой субстанции (тепло, легкие суспензии и пр.) в направлении, обратном градиенту насыщения, имеет следующий вид:

Не излагая всех имеющихся приемов решения этой задачи, приводим только конечное уравнение распределения твердых частиц М. А. Великанова, который распределение скоростей принял по Ясмунду — Никурадзе
Диффузионная теория подтверждается опытными данными при малых насыщениях потока мелкими частицами). Эта теория решает только один вош рос из большого числа вопросов теории взвесе- несущих потоков, а именно: вопрос о распределении концентрации твердых частиц по сечению турбулентного потока. Этот вопрос решается для малой насыщенности турбулентного потока мелкими твердыми частицами. В такой постановке эта задача мало интересна для практических проблем гидротранспорта, поскольку гидротранспорт в основном представляется потоками гидросмеси значительной средней консистенции. Однако поток гидросмеси имеет сложную структуру: придонная область занята гидросмесью, перенасыщенной преимущественно крупными твердыми частицами, если таковые вообще имелись в исходном грунтоматериале. Верхние слои потока переносят мелкие частицы при их незначительной концентрации в жидкости. К этой области может быть вполне применима диффузионная теория.
Гравитационная теория движения взвешенных наносов
Вся положительная работа силы тяжести при равномерном движении однородной жидкости в безнапорном потоке расходуется на преодоление силы сопротивления.
М. А. Великанов впервые высказал мысль, что при транспортировании твердых частиц (например, песка) в водном турбулентном потоке часть энергии потока должна затрачиваться на поддержание твердых частиц во взвешенном состоянии. Этот бесспорный факт вызвал острую дискуссию, причем не по существу самого факта, а по вопросу места работы взвешивания в энергобалансе взвесенесущего потока. Работу взвешивания в единицу времени, отнесенную к элементарному объему бхХ ХМ- М. А. Великанов оценивает выражением в рассматриваемом элементарном объеме твердых частиц.
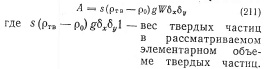
М. А. Великанов утверждал, что эта работа взвешивания должна добавляться к работе сил сопротивления и, следовательно, безнапорный поток, несущий твердые частицы, при той же глубине и при том же. уклоне должен обладать меньшей скоростью, чем поток чистой воды. Он придерживался мнения, что работа взвешивания берется из энергии осредненного движения. Другие исследователи (например, И. Г. Баренблатт) считают, что работа взвешивания берется из энергии пульсационного движения.
Подход М. А. Великанова к решению этой задачи состоит в следующем. Поток делится на две части, как бы на два самостоятельных потока. Один поток представлен жидкой фазой без твердых частиц, вследствие чего плотность его будет меньше плотности жидкой фазы и равна р0 (1—s). Этот поток жидкой фазы является активной частью дисперсоида, которая переносит во взвешенном состоянии твердые частицы. Второй поток лишенный несущего его субстрата, состоит из твердой фазы, плотность которой равна произведению pTB-s. В качестве третьего, суммирующего потока рассматривается движение дисперсоида, состоящего из смеси однородной жидкости с твердыми частицами.
Жидкая составляющая рассматривается как активная часть дисперсоида, переносящая твердую составляющую потока благодаря наличию поперечного перемешивания жидкости. Причем принимают, что твердые частицы имеют одинаковую гидравлическую крупность и движение считается плоским, равномерным, с установившейся консистенцией.
М. А. Великанов считает, что работа взвешивания получается как за счет уменьшения пульсационной энергии, так и за счет возрастания осредненной. Следовательно, совершенно правомерно включение работы взвешивания в энергобаланс осредненного движения.
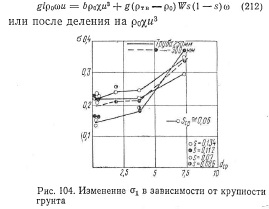

Результативным уравнением гравитационной теории явилось выражение для определения консистенции в точках сечения потока
При принятых предположениях допускается постоянство значений о (для мелких частиц малая изменчивость от подтверждена экспериментальной проверкой).
По данным В. С. Кнораза и Н. С. Блетч М. А. Великанов нашел, что о—0,204: const. Из выражения (214) получим

2. Чем выше средняя консистенция потока, мельче песок и выше средняя скорость потока, тем выше потолок взвешивания, и наоборот.
3. При транспортировании непромытых песков, содержащих илистые частицы, последние могут насыщать пространство над потолком взвешивания песчаной фракции, что может свидетельствовать о наличии некоторого, возможно весьма незначительного турбулентного перемешивания в этих верхних слоях потока.
4. Наличие мелких фракций в верхних слоях потока не противоречит факту преобладания векторов локальных скоростей в потоке гидросмеси над векторами скоростей в потоке чистой воды, рассматриваемых в одной и той же точке пространства, заполненного движущейся жидкостью.
5. Если твердая составляющая гидросмеси—кварцевый песок, то можно принять
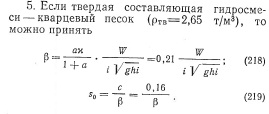
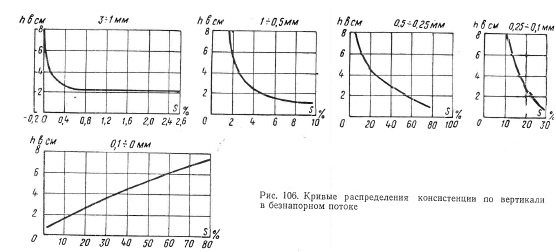
Значение коэффициента полезного действия о было подсчитано позднее по другим опытным данным гидротранспорта. Оказалось, что а зависит от крупности твердых частиц (рис. 104), и его значение можно условно принять постоянным при t/s-C 3 мм (точки на графиках представляют собой результат осреднения из большего числа опытных данных). Установлено также, что на параметр о влияют консистенция гидросмеси и диаметр трубопровода.
Основной параметр гравитационной теории (3 до значений d.3 мм не зависит от гидравлической крупности W, для больших значений d параметр возрастает (рис. 105).
На основании исследований гидротранспорта и особенно наблюдений за характером движения гидросмеси через прозрачные вставки в трубопроводах можно сделать следующие выводы. При транспортировании чистого (промытого) песка по горизонтальным трубам насыщаются песком только нижние слои потока. Над потолком взвешивания, представляющим ясно различимую границу зоны, которая насыщена песком, течет технически чистая вода.
6. Течение под потолком взвешивания влияет на течение над потолком взвешивания, поэтому параметр Кармана для течения над потолком отличается от значения этого параметра для равномерного потока чистой воды.
7. Значение параметра Кармана для течения под потолком взвешивания меньше, чем для потока над ним.
Кривые распределения консистенции по вертикали в безнапорном потоке приведены на рис. 106.
В заключение необходимо отметить, что диффузионная и гравитационная теории имеют правильное физическое построение, но применение их ограничено областью малых консистенций и преимущественно наличием мелких наносов. Основы этих теорий сыграли большую роль в построении инженерных методов расчета напорного и безнапорного гидротранспорта.
