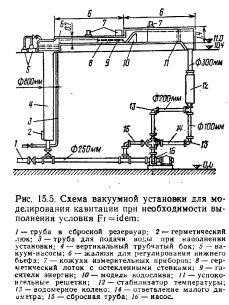
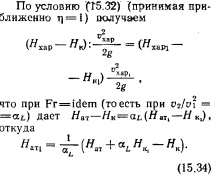Гидравлическое моделирование
Критерии подобия гидравлических явлений и их роль в различных случаях. В 15.1.2 указывалось, что при моделировании гидравлических явлений в общем случае надо учитывать безразмерные параметры Fr, Re, Eu, Sh, а иногда и We. Кроме того, для многих гидравлических задач существенную роль играет относительная шероховатость К/R (где К — абсолютная шероховатость, R — гидравлический радиус), а для турбулентных потоков (особенно с высокой турбулентностью) — число Кармана Ка—критерий турбулентности. Этот критерий (для соблюдения подобия он должен быть одинаковым для натуры и модели) можно представить в таком виде:

Таким образом, в общем случае критериальное уравнение для гидравлических процессов можно записать в таком виде (для жестких моделей, то есть не рассматривая пока условия размываемости русла и транспорта наносов) :
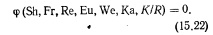
В зависимости от вида рассматриваемых течений те или иные из этих критериев выпадают или их можно не учитывать, так как они оказывают несущественное влияние. Так, число Струхаля Sh надо использовать при рассмотрении неустановившихся течений (или пульсационных характеристик потока). Число Вебера We в большинстве случаев можно не учитывать вообще и тем более при моделировании не бывает необходимости ставить условие We=idem, Этот критерий оказывает некоторое влияние на явления кавитации, а также распада струй и аэрации, и его в ряде случаев учитывают при исследовании.
Число Кармана Ка вообще подлежит учету при моделировании турбулентных потоков, однако в практике обычно не пытаются жестко соблюдать требование Ka = idem, что связано как с трудностью его реализации, так и с тем, что при соблюдении других требований (Re>Rerp, крупномасштабные модели и др.) это условие с приемлемым для практических целей приближением выполняется. При исследовании местных сопротивлений, коротких участков сооружений (например, оголовков водосливов), участков малой протяженности сильно турбу- лированных потоков (гидравлический прыжок) можно обычно не учитывать при моделировании относительную шероховатость и не ставить условие К= = idem или K/R=idem. При напорных установившихся течениях практически обычно выпадает и критерий Фруда (автомодельность по Fr), то есть критериальное уравнение можно принимать в виде:
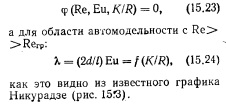

причем, как указывалось выше, в ряде случаев нет необходимости учитывать (моделировать) относительную шероховатость, то есть параметр выпадает из этой зависимости. В области автомодельности выпадает критерий Рейнольдса, от которого уже перестают зависеть результаты исследований, и условие Eu = idem соответствует здесь требованию A,=idem, которое должно выполняться для русл достаточной протяженности (то есть требуется подбор шероховатости на модели). Шероховатость часто подбирают по данным, полученным для равномерного движения (что в общем случае неравномерного движения приближенно), например по графику А. П. Зегжда, а при образовании гряд—по графику Н, С. Знаменской [43].
Метод масштабных серий. В ряде случаев исследуют несколько геометрически подобных моделей разных масштабов (масштабная серия) и полученные в опытах характеристики экстраполируют на натуру. Найденные зависимости позволяют вносить масштабные поправки в соответствующие характеристики, полученные на небольших моделях, на которых не обеспечена автомодельность по числу Рейнольдса. Такую методику можно использовать при исследовании напорных водоводов [111], водосливов и других объектов.
Формулы для масштабных поправок даны [24, 45] для вакуумных водосливов и входных оголовков безнапорных труб Н. П. Розановым, для безвакуумных профиля Кригера— Офицерова — Н. А. Петровым, для водосливов с широким порогом—А. Р. Березинским, для шахтных водосбросов — П. П. Мойсам [53]. Численно они мало разнятся друг от друга.
Явление истечения через водослив подчиняется закону гравитационного подобия (Фруда), и если непромоде- лированные силы вязкости и поверхностного натяжения существенно не влияют, то коэффициент расхода или коэффициент вакуумности не зависит от масштаба модели. Влияние масштаба обусловлено влиянием указанных второстепенных сил. Масштабные поправки устанавливают от безразмерного критерия, характеризующего тр силы, которые являются следующими по значимости для данного явления после сил тяжести. В данном случае ими будут силы вязкости, и поэтому поправки вносят в зависимости от числа Рейнольдса.
Для масштабной поправки вакуумных водосливов с круговым оголовком Н. П. Розановым получена следующая зависимость:

Коэффициент расхода для натуры коэффициент расхода модели.
Из зависимости (15.28) следует, что при коэффициент расхода модели тх всего и на 1 % меньше, чем для натуры (то есть при больших Re).
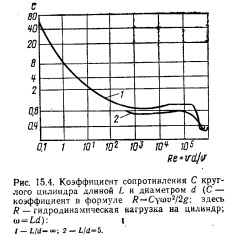
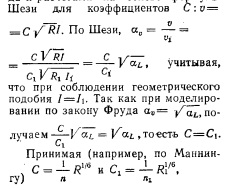

При исследовании на моделях относительно протяженных участков рек часто из-за ограниченных размеров экспериментальной площадки или лотка масштаб модели получается мелким, что приводит к очень малым глубинам и скоростям потока при соблюдении геометрического подобия. При этом может оказаться, что Re
Очевидно, что при искажении масштабов уклон. Необходимо, чтобы на модели сохранялось спокойное течение если оно обычно такое же для натуры, иначе качественно изменится характер течения.
При искажении масштабов изменяются некоторые масштабные коэффициенты по сравнению с указанными в таблице 15.1.
Моделирование водных потоков с деформируемым руслом и твердого расхода. При проведении исследований на неразмываемых (жестких) моделях о величинах вероятных русловых деформаций можно судить лишь ориентировочно — по сопоставлению замеренных (пересчитанных в натуру по закону гравитационного подобия) скоростей с неразмывающими скоростями для данных грунтов или креплений, если последние проектируют. Количественных данных о величинах русловых деформаций (размывов и отложений) эксперимент на жесткой модели непосредственно не дает или дает не полностью, и то только для размывов, если проводить исследования по методике А. Д. Халтурина с постепенным «подскребыванием» русла модели (выполненного из неразмыва- емого, но легко счищаемого материала, например тощего цементного раствора) в тех местах, где скорости больше промоделированных неразмываюших скоростей добиваясь, чтобы везде было выполнено условие. Поэтому изучение русловых деформаций проводят обычно на моделях с размываемым руслом.
Условие моделирования размываемости (или неразмываемости) грунта можно записать в таком виде:

Другая картина получается, если моделируется русло равнинной реки, сложенное мелкими наносами, и масштаб модели приходится принимать довольно мелкий (ограниченные размеры лаборатории, моделируется крупная река и т. д.). С такой малой допускаемой скоростью невозможно подобрать грунтовой материал для модели. В подобных случаях приходится переходить на приближенное моделирование с искажением масштабов (ah При исследованиях русловых деформаций на участках достаточно большой протяженности надо соблюсти условие и иметь достаточное соответствие с натурой коэффициентов сопротивления (учитывая и повышение сопротивлений на пойменных участках реки и др.). Часто при исследовании русловых деформаций используют морфологические зависимости между элементами русла (например, С, Т. Алтунина,В.М. Лохтина, гл. 10.1), а также и и методику так называемого натурального моделирования, при которой в лаборатории создают и изучают «малую реку», процессы деятельности которой должны качественно соответствовать реке в натуре. Если при моделировании использовать, например, морфологическую зависимость (10.2) с обозначениями по рисунку 15.1 и принять, то получим, откуда требующееся искажение масштабов. Для высокогорных участков рек m = 1, и искажения масштабов не требуется При исследовании размываемых моделей часто моделируют и расход наносов (твердый расход) Р, а также время продолжительности деформаций т. При этом используют соответствующие зависимости для твердого расхода— Эйнштейна, И. В. Егиазарова, И. И. Леви [43]. Если модель исследуют без искажения масштабов при искажении масштабов приведены в [43]. Там же приводятся рекомендации по моделированию потоков большой мутности (токов плотности). В случаях моделирования местных размывов, например в НБ водосбросных сооружений, надо соблюдать критерии (обычно приближенно удовлетворяется при не слишком малых Re). Если необходимо учесть и взмучивание мелких частиц (например, их попадание в водозабор), то ставится также условие, где масштабный коэффициент гидравлической крупности. Местные размывы, как правило, не изучают на моделях с искажением масштабов. Большую сложность представляет моделирование размывов скальных грунтов. Скальные блоки — отдельности, выделяемые трещинами — иногда заменяют при моделировании эквивалентными по массе частицами несвязного грунта (обычно гравия), что весьма условно, хотя для Красноярского гидроузла и дало результаты по размывам, в основном соответствующие происшедшим затем в натуре. Иногда в лаборатории отдельности скалы воспроизводят соответствующими плитками, не связанными друг с другом или имеющими слабый связующий заполнитель в контактах. Методы моделирования размыва скалы требуют дальнейшей разработки. Исследование волновых процессов [43]. Волны в лаборатории создают специальными волнопродукторами, причем стремятся получить форму волн, подобную натурной. Основным критерием моделирования является критерий Фруда (15.10), широко используют критерий Струхаля (15.17), обычно соблюдают геометрическое подобие, но иногда и допускают некоторое искажение масштабов. При волнах малой высоты могут оказывать влияние числа Вебера (влияют силы поверхностного натяжения). Моделирование безнапорных потоков на напорных моделях. Сущность этого приближенного метода моделирования [43, 45] состоит в том, что на модели по ожидаемой свободной поверхности безнапорного потока располагают стекло (или оргстекло), и модель превращается в напорную. Через модель обычно пропускают воздух (воздушная модель), редко воду (водная модель). Так как в модели, сравнительно небольших размеров можно задавать большие скорости течения, легко осуществить требование работы в области автомодельности (Re>Rerp) и обеспечить подвижность частиц при моделировании размываемых русл. Воздушные модели получаются портативными и относительно недорогими. Иногда считают [43], что при таком моделировании не будет больших ошибок при (автомодельность по критерию Фруда). Масштаб расходов получается как отношение расхода исследуемого водотока к расходу воздуха (или воды) на модели; масштаб скоростей, а при неискаженной модели а0—асз/а 1. Расширить область применения напорных моделей на случаи безнапорных потоков со значительной кинетичностью и неустановившихся можно при использовании не жесткой (стекло), а упругой свободной поверхности [45]. Воздушное напорное моделирование с успехом применяют для исследования различных плановых задач (пропуск паводков по пойме, изучение компоновок гидроузлов, речных водозаборов, прудов-охладителей, стеснений русла перемычками и др.), особенно для предварительных стадий проектирования. Напорные водяные модели использовали при изучении русловых процессов при строительстве Кизил- Аякского гидроузла на Амударье, занесения поймы р. Оки песком. Однако водяные напорные установки более сложны в конструктивном оформлении и эксплуатации, поэтому их применяют редко. Моделирование кавитации. При моделировании кавитации в напорных потоках ставится условие одинаковости параметров кавитации для модели и натуры, то есть При моделировании кавитации в безнапорных потоках, когда необходимо соблюсти закон гравитационного подобия (например, при исследовании кавитации гасителей в гидравлическом прыжке), надо ставить также и условие Fr — idem, а в общем случае и Ка = idem. Исследования в этом случае надо проводить в специальном герметически закрытом вакуумном стенде, внутри которого над свободной поверхностью потока должно быть некоторое разрежение, то есть атмосферное давление модели должно быть меньше атмосферного давления в натуре (рис. 15.5). Практически при исследованиях обычно поступают таким образом: при заданных условиях (расход, глубина в НБ и т.д.) изменяют значения и устанавливают момент возникновения кавитации, то есть определяют. Затем значение сравнивают с параметром кавитации, подсчитанным для натуры, и по зависимости (4.13) устанавливают, следует ли ожидать кавитацию в натуре. Краткие сведения о технике проведения гидравлических исследований. Модели гидроузлов и свободных рек обычно испытывают на специальных экспериментальных площадках, иногда в широких гидравлических лотках, а очень крупные модели — не в закрытых помещениях, а на специальных площадках под открытым небом. Например, модель р. Миссисипи (лаборатория в Джексоне, США, имела длину 1 371 м и ширину 1 066 м и была расположена на открытой площадке площадью 89 га. Фрагменты сооружений часто исследуют в гидравлических лотках. Устраивают (на площадках) и специальные установки, например моделирующие водосброс с воспроизведением участков верхнего и нижнего бьефов и сбросного тракта в виде прозрачной (обычно из оргстекла) трубы, моделирующей туннель, или лотка (при открытом водосбросе). Модели выполняют из различных материалов—бетона, дерева, стали, оргстекла и др. Глубины потока измеряют шпиценмасштабами, иногда поплавковыми и другими устройствами с автоматической записью показаний; скорости — поплавками, гидрометрическими трубками, микровертушками. При измерении мгновенных скоростей (или пульсаций скоростей) используют гидрокинематические жидкие и твердые шарики —индикаторы, применяя киносъемку, микровертушки, датчики скорости, а иногда — гидроанемометры,не получившие, однако, широкого распространения, и лазеры. Осредненные давления измеряют с помощью пьезометров, пульсирующие (или пульсаци- онные составляющие) —специальными датчиками. Волны на моделях создаются волнопродукторами. На воздушных моделях скорости измеряют скоростными трубками, термоанемометрами, аэрометрическими вертушками, фотоискровым способом (линии тока прочерчивают по струям выпускаемого дыма), а давления — манометрами и датчиками. При кавитационных исследованиях, кроме обычной аппаратуры, применяют также ультразвуковую, вакуумметры, высокочастотную киносъемку и др. Расходы воды при гидравлических исследованиях замеряют мерными водосливами, диафрагмами, водомерами Вентури, иногда объемным или весовым способом. Более подробные сведения о технике и методике проведения гидравлических исследований приводятся в специальной литературе [43, 45 и др.].