
Расчет казуальной фильтрационной прочности основания плотины
Следует различать два возможных вида нарушения фильтрационной прочности грунта основания:
1) нарушение нормальной фильтрационной прочности, которое может происходить в заранее известных наиболее слабых местах рассматриваемого поперечного профиля основания при известных расчетных условиях в этих местах, например: а) на контакте дна нижнего бьефа и покрывающего его обратного фильтра; б) в области выходного фрагмента основания, где может произойти выпор грунта; в) на контактах крупнозернистых и мелкозернистых грунтов, слагающих основание, и т. п.;2) нарушение казуальной фильтрационной прочности грунта основания, которое может происходить в местах продольного профиля, заранее не известных; расчетные условия для оценки такой прочности в этих местах могут носить в некоторой мере неопределенный, случайный характер. В качестве примера нарушения такой прочности можно привести образование в отдельных местах продольного профиля, плотины поперечных ходов сосредоточенной фильтрации под плотиной вследствие ряда причин: а) случайной недоброкачественности производства работ; б) неучтенной неравномерной осадки плотины; в) внутренней суффозии, обусловленной неучтенной неоднородностью грунта; г) осадки грунта под плотиной в пределах горизонтальных элементов контура при отсутствии осадки самой плотины и т. п. Вопрос о казуальной фильтрационной прочности грунта основания непосредственно связан с вопросом надежности сооружения.
Казуальная фильтрационная прочность основания плотины может быть оценена только приближенно тем или другим гидродинамическим параметром, характеризующим весь фильтрационный поток в целом. В качестве такого параметра следует принимать некоторый средний пьезометрический уклон (градиент напора) iK, который может быть назван пьезометрическим уклоном, контролирующим казуальную прочность.
Форму и размеры подземного контура надо назначать в соответствии с расчетом казуальной фильтрационной прочности. Установленный таким образом контур необходимо дополнительно проверять на нормальную прочность (см. § 17.7).
2. Расчет казуальной фильтрационной прочности по методу контролирующего градиента. Исходя из рассмотрения казуальной фильтрационной прочности, размеры и форму контура в общем ‘случает следует устанавливать путем подбора, добиваясь соблюдения условия

Определение контролирующего градиента iK:


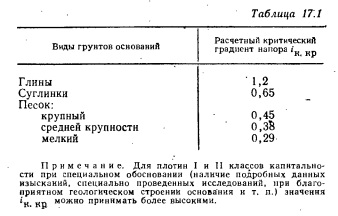
Предварительно размеры подземного контура назначают, исходя из казуальной фильтрационной прочности грунта основания. При этом пользуютсяследующими зависимостями:
а) сильно распластанная схема контура, когда ?к = гг.к В этом случае минимально допускаемая длина подземного контура оказывается равной

Разумеется, формулы (17.45) и (17.48) в некоторых случаях приходится решать подбором в связи с отсутствием в начале расчета данных;
б) общий случай схемы подземного контура, отличной от чистого шпунта и не удовлетворяющей условию (17.35),

При относительно неглубоком залегании действительного водоупора можно принять равной и переписать формулу (17.50) в виде
По этой формуле легко можно найти минимально допускаемое значение 2, а затем подобрать подземный контур так, чтобы суммарный коэффициент сопротивления его не был меньше найденного.
При относительно глубоком залегании действительного водоупора зависимость (17.50) приходится переписать:
Определив по формулам (17.53) и (17.54) значение, подбирают контур так, чтобы он характеризовался значением, равным найденному;
в) случай чистого симметричного шпунта при глубоком залегании действительного водоупора; при 0,4...0,5 минимальную допустимую глубину забивки шпунта в соответствии с зависимостями (17.32) и (17.42) находят по формуле
