Построение пространственных конфигураций в форме выпуклых многогранников
Системы из дискретных элементов на плоскости могут образовывать регулярные и нерегулярные плоские точечные решетки. С позиций определения кристаллографических классов точечные решетки в трехмерном пространстве приводятся к пяти правильным многогранникам, называемым Платоновыми телами, и к 13 полуправильным многогранникам, известным под названием тел Архимеда. Каждая из этих конфигураций может быть вписана в шар.
Гранями правильных тел трехмерного пространства являются правильные многоугольники. Поскольку в каждой вершине многогранника сходятся, по меньшей мере, три многоугольника, то углы его должны быть меньше, чем 2л/3. Следовательно, гранями правильных многогранников могут быть только равносторонние треугольники, четырехугольники и пятиугольники.
Правильные многогранники переходят друг в друга при полярном преобразовании относительно вписанного или описанного шара. При этом тетраэдр (Т) занимает особое место, так как он двойственен самому себе, между тем как остальные четыре тела попарно двойственны друг другу: октаэдр (О) — гексаэдру (Г), а додекаэдр (Д) — икосаэдру(1).
Следует также отметить, что не все из правильных многогранников, рассматриваемых как пространственные точечные решетки, удовлетворяют условию геометрической неизменяемости; в действительности только три из них, имеющие треугольную разрезку (тетраэдр, октаэдр и икосаэдр) и обозначенные соответственно буквами Т, О и I, геометрически неизменяемые и статически определимы.
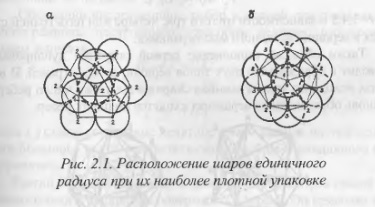
При решении экстремальной задачи о наиболее плотной решетчатой упаковке шаров единичного радиуса доказывается [30], что такое расположение может быть достигнуто, когда центры шаров образуют кубооктаэдр так, что каждый шар касается 12 других, а именно: шести — экваториальных, трех — нижнего слоя и трех — верхнего (рис. 2.1,а).
Кубооктаэдр относится к семейству равноугольных полуправильных многогранников и полярным преобразованием относительно описанного шара переводится в двойственный ему равногранный многогранник — ромбододекаэдр.
Можно также получить другое компактное расположение шаров, если центральный переместить таким образом, чтобы остальные 12 соприкасающихся с ним шаров с их центрами на вершинах кубооктаэдра сблизились между собой в образовавшемся пространстве. При такой упаковке кубооктаэдр преобразуется в икосаэдр (рис. 2.1,6), где шар касается 12 других, равных ему шаров, в вершинах вписанного икосаэдра.
Таким образом, каждая система материальных шаров в пространстве разбивает его на выпуклые многогранники.
Различают 4 способа построения пространственных конфигураций, которые приводят к образованию семейств полуправильных многогранников, обеспечивающих различные приближения к вписанной сфере S [34].
Первый — заключается в проецировании на поверхность сферы S середин ребер многогранника из центра вписанной сферы. Такой прием построения конфигураций точек и плоскостей в пространстве носит название способа дублирования.
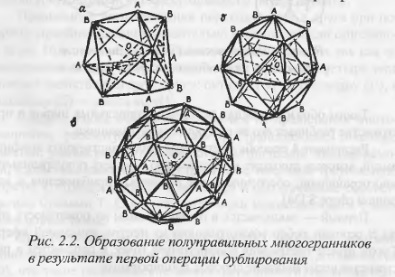
Если дублирование применяется к определенному типу правильных или полуправильных многогранников, то в результате получается ряд пространственных конфигураций, которые обозначаются символом исходного многогранника и снабжаются индексом 2п, причем показатель степени n соответствует порядковому номеру операции. Так, например, после первой операции дублирования, примененной к правильным многогранникам, имеющим Е вершин, К ребер и F граней, получим полуправильные многогранники (рис. 2.2, а, б, в), у которых число вершин, ребер и граней в свою очередь будет равно:
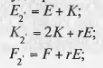
где r=3,4,5 в зависимости от того три, четыре или пять граней сходятся в вершине исходного многогранника.
Таким образом, выполнение первой операции дублирования приводит к образованию двух типов вершин, ребер и граней. В вершинах исходного многогранника сохраняется то же число ребер, а во вновь образованных вершинах сходятся по шесть ребер.
В общем случае, применение дублирования всегда связано с сохранением числа правильных многоугольников исходного многогранника, причем они являются либо прямым, либо обратным отображением граней исходной фигуры.
Второй способ построения пространственных конфигураций, носящий название способа деления, состоит в делении дуг большого круга, соответствующих каждому из ребер исходного многогранника, на равные части, что эквивалентно выполнению первой операции дублирования. При этом в вершинах правильных многогранников число ребер и граней остается постоянным. Последние представляют собой равнобедренные треугольники. Кроме того, появляется новый тип граней, каждая из которых имеет удвоенное число сторон, причем противоположные стороны параллельны, но не равны друг другу.
Обозначив число вершин, ребер и граней полуправильного многогранника, построенного способом деления, индексом 3', можем записать
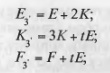
Здесь t указывает на какое нечетное число равных частей делятся дуги большого круга, соответствующие ребрам правильного многогранника.
Третий способ заключается в проецировании центров граней правильного многогранника на поверхность сферы S. Он приводит к построению двух спаренных многогранников, называется процедурой сдваивания и характеризуется взаимным проникновением двух вписанных в сферу многогранников.
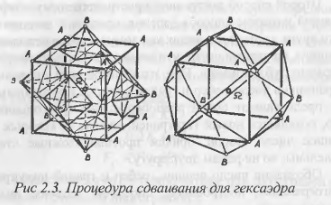
Применительно к гексаэдру (С) (рис. 2.3) полученная таким образом конфигурация представляет собой двойной многогранник СО, соединение вершин которого дает полуправильный многогранник с пирамидами на гранях гексаэдра.
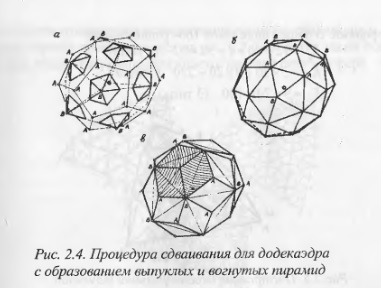
В случае додекаэдра (D) этот способ приводит к образованию двойного многогранника DI (рис. 2.4,а). Вершины двух спаренных многогранников здесь также могут бьгть соединены между собой в определенной последовательности. При этом сохранение ребер D привело бы к образованию полуправильного многогранника на основе выпуклых пирамид (рис. 2.4,6). Подобно этому, сохраняя ребра 1, получают новую конфигурацию в виде совокупности вогнугых пирамид (рис. 2.4,в).
Рассмотрение пространственных конфигураций с более мелкой разрезкой, полученных способом сдваивания, показывает, что основной недостаток его, во-первых, выражается в образовании вершин с большим числом сходящихся в них ребер и, во-вторых, в получении многочисленных типоразмеров ребер.
Наконец, четвертый способ построения пространственных конфигураций сводится к образованию пирамидальных элементов для многогранников с нетреугольными гранями. Он называется способом построения пирамид, заключается в проецировании центров квадратных и пятиугольных граней многогранников из центра вписанной сферы S и приводит к образованию пространственных конфигураций, характеризуемых наличием треугольных граней в виде равносторонних и равнобедренных треугольников.
Наилучшим образом задача построения пространственных конфигураций в форме выпуклых многогранников решается способами дублирования и построения пирамидальных элементов. При этом треугольные сферические решетки получаются в тех случаях, когда процедура дублирования применяется к икосаэдру или же способ построения пирамид — к додекаэдру (D).
Следует также заметить, что для полурегулярных многогранников применение этих способов ограничено классом фигур типа А (3,5,3,5), А (5,6,6) и А (3,3,3,3,5), имеющих только треугольные, пятиугольные и гексагональные грани.
Пространственные точечные решетки, приводящие к образованию конструктивной сети многогранного купола, описываются впоследствии как икосаэдральные, додекаэдральные и решетки типов А (3,5,3,5), А (5,6,6) и А (3,3,3,3,5).
Для более наглядного представления о дискретных точечных фигурах и с целью облегчения при определении количества типоразмеров их ребер и граней построения решеток выполняются на одной из граней многогранника.
Пример икосаэдральной точечной решетки, получаемой в результате деления дуг большого круга на три равные части, приведен на рис. 2.5. В самом деле, проектируя центры ы треугольных граней икосаэдра ААА из центра Q на S и соединяя С с D, имеем конфигурацию, соответствующую полуправильному многограннику, в состав которой вход ят пятиугольные пирамиды на вершинах и шестиугольные — с основаниями в виде плоских шестиугольников с параллельными, но неравными противолежащими сторонами. В общем виде такой 180-гранник имеет:
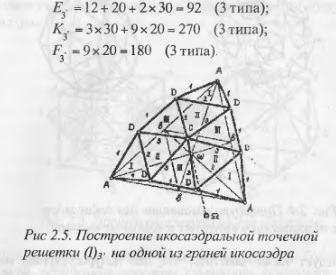
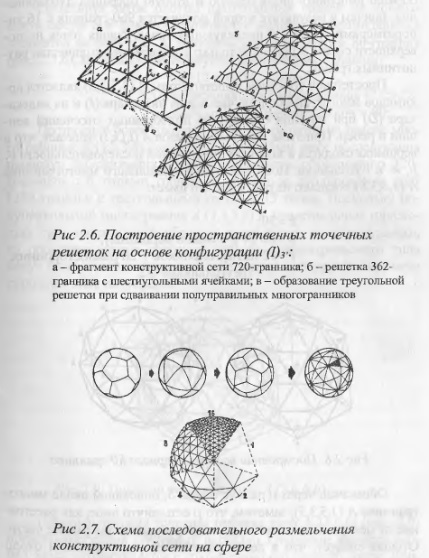
Выполнение над построенной конфигурацией процедуры дублирования, приводит к 720-граннику, имеющему 8 типоразмеров ребер (рис. 2.6,а). На его основе получается также полуправильный многогранник с правильными пятиугольными гранями у вершин 1 и несимметричными шестиугольниками семи типов на остальной поверхности, причем два из них обратны друг другу (рис, 2.6,6). Полученный 362-гранник имеет 11 типов ребер. Два полуправильных многогранника могуг быть сдвоены, что дает треугольную точечную решетку (рис 2.6,в).
За рубежом наибольшее распространение получил способ построения конструктивной сети, основанный на триангуляции поверхности сферы с помощью геодезических линий, и носящий название способа Б. Фуллера [22]. В данном случае также используется разрезка поверхности сферы на 20 равносторонних сферических треугольников, проекции которых на соответсгвующие плоскости приводят к образованию кристаллического икосаэдра. Далее отдельные сферические треугольники разделяются на три конгруэнтных сферических четырехугольника, являющиеся один по отношению к другому зеркальным отображением. Суть этого способа, предусматривающего использование процедур сдваивания и деления, хорошо прослеживается на рис. 2.7, где дается также схема последующего разукрупнения конструктивной сети на сфере.
Что касается додекаэдральных точечных решеток, то исходной фигурой для их построения является полуправильный многогранник, изображенный на рис. 1.4.6. Над таким многогранником целесообразно выполнить лишь первую и вторую операции дублирования, причем в результате второй получается 960-гранник с 16 типоразмерами граней, и последующая триангуляция точек на поверхности сферы S приводит только к увеличению количества разнотипных граней.
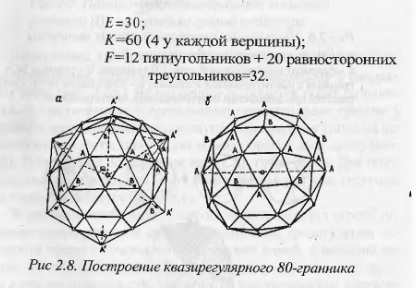
Простейшей точечной решеткой типа А (3,5,3,5) является архимедов многогранник, получаемый из икосаэдра (Г) и из додекаэдра (D) при помощи специально подобранных отсечений вершин и ребер. При этом, например, символ А означает, что в вершинах сходятся в заданной циклической последовательности i-, j- и k-угольники. Построение полуправильного многогранника А (3,5,3,5) показано на рис. 2.8,а. Он имеет: