
Понятие о механике разрушения бетона
Одним из путей ускорения научно- технического прогресса в строительстве является повышение прочности бетона и оптимизация его деформативных свойств. Уже в двенадцатой пятилетке ставится задача производства бетонов прочностью до 100 МПа; к 2000 г., согласно современным научным прогнозам, предполагается создание специальных бетонов прочностью до 400 МПа и рядовых до 140 МПа. Однако на этом пути возникает много сложностей, связанных с необходимостью яснее представить себе природу прочности бетона. И если наши знания о прочности и причинах разрушения металлов в настоящее время достаточно глубоки (ведь классическая теория упругости, а затем теория пластичности развивались применительно к свойствам металлов), то с бетоном дело обстоит намного сложнее. Для бетона до сих пор еще не создано законченной теории деформирования и разрушения, а чисто эмпирический путь поиска новых высокопрочных составов бетона весьма трудоемок и не всегда приводит к цели. Еще труднее чисто эмпирическим путем подойти к решению актуальнейшей задачи современной науки о материалах — прогнозированию механических характеристик материала и созданию материала с заранее заданными (в некоторых пределах) свойствами.
Вместе с тем большие возможности в области прогнозирования механических свойств бетона открывают методы современной, быстро развивающейся отрасли науки — механики разрушения, рассматривающей процесс разрушения на различных уровнях структуры материала, начиная с атомно-молекулярного.
Первые представления об атомном строении материи принадлежат Демокриту (460...370 гг. до н.э.) и Лукрецию (95...55 гг. до н. э.). Эти представления были полностью построены на догадках. Тем не менее Лукрецию удалось предугадать, что между атомами вещества существуют силы сцепления, связывающие эти атомы в единое целое. Столетия, прошедшие после эпохи Демокрита и Лукреция, не смогли внести практически ничего нового в понимание атомного строения вещества и его связи с прочностью твердых тел.

Правда, после открытия атомного строения вещества некоторые ученые, основываясь на характере межатомных взаимодействий, пытались определить теоретическую прочность материала, т. е. величину напряжений, необходимых для взаимного разделения двух соседних атомных молекулярных слоев в твердом теле. При этом предполагалось, что материал не имеет никаких дефектов структуры, т. е. все атомы (молекулы) расположены в определенном порядке (рис. 1.3, а, б). При таких предположениях расчеты показывали, что теоретическая прочность составляет 10.. .20 % от важнейшей константы— модуля упругости материала (Е). Например, у стекла Е = 70 000 МПа. Поэтому теоретическая прочность стекла = 14 000 МПа, что почти в 100 раз выше реальной (технической) прочности стекла, измеряемой при обычных испытаниях (30...200 МПа). Такое же соотношение между теоретической и технической прочностью получалось и для других материалов.
Исследования А. Гриффитса. Английский ученый А. Гриффитс (1893— 1963) рассматривал процесс разрушения хрупкого материала (например, стекла), сопровождающийся развитием трещин. При этом он исходил из основополагающего закона природы — закона сохранения и превращения энергии. Главная идея состояла в том, что потенциальная энергия тела, накопленная им в процессе упругого деформирования перед разрушением, полностью превращается при разрушении в другой вид энергии, а именно в поверхностную энергию образующихся новых поверхностей.
Гриффитс нагревал стеклянные стержни посередине и оттягивал их концы, получая нити — волокна различного диаметра. Он установил, что прочность существенно зависит от диаметра — чем тоньше полученные нити, тем больше напряжения, необходимые для их разрыва. Сначала прочность нитей увеличивалась медленно, но затем кривая зависимости прочности от диаметра поднималась чрезвычайно круто. Экстраполируя эту кривую в область крайне малых диаметров, Гриффитс получил для прочности тончайших нитей величину 11 000 МПа, что было близко к теоретической прочности стекла (14 000 МПа).
Для теоретического истолкования полученных результатов Гриффитс использовал понятие о концентрации напряжений. Число, показывающее, во сколько раз напряжение около концентратора (отверстия) превышает номинальное (т е. в гладкой пластине), называется коэффициентом концентрации напряжений. В случае достаточно широкой пластины и кругового отверстия коэффициент концентрации равен 3,0. В случае эллиптического отверстия коэффициент концентрации напряжений равен 1+2 a/b, где а, b — размеры главных полуосей эллипса. Гриффитс предположил, что трещины являются сильно вытянутыми эллипсами. Соотношение полуосей a/b для трещины, например, длиной 10 мкм и шириной 0,1 мкм равно 100:1; коэффициент концентрации напряжений в этом случае будет равен 201. При подобной концентрации напряжений теоретическая прочность стекла (14 000 МПа) должна снизиться примерно до 70 МПа, что близко к прочности обычного стекла. Гриффитс пришел к выводу, что в обычном стекле существует множество тончайших трещин, не поддающихся обнаружению, причем в тонких волокнах эти трещины образуются реже.
Физическую картину того, что происходит на атомарном уровне вследствие концентрации напряжений у кончика трещины, иллюстрирует схема на рис. 1.3, в, г. Если растущая трещина перерезала несколько межатомных связей (см. рис. 1.3, в), то в результате концентрации напряжений существенно возросла нагрузка, передаваемая на атомную связь у самого кончика трещины (см. рис. 1.3, г). В таких условиях перегруженная связь, как правило, не выдерживает и разрывается, что приводит к перегрузке следующей связи и т. д. Таким образом, при наличии трещины сравнительно небольшая внешняя нагрузка разрушает сильнейшие межатомные связи, приводя к полному разделению образца материала на части. Но как и при каких условиях начинается движение существующих в материале начальных трещин? Гриффитс показал, что рост трещины обязательно должен являться энергетически выгодным процессом (количество запасенной в теле энергии уменьшается).
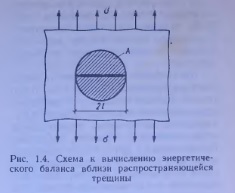
Рассмотрим энергетический баланс тела, в котором распространяется трещина (рис. 1.4). В процессе движения трещины участок материала, непосредственно примыкающий к ее краям, разгружается — релаксирует (заштрихованная область на рис. 1.4). Это означает, что напряжения и деформации в нем уменьшаются, а упругая энергия, запасенная в этой зоне тела, высвобождается. Если принять согласно рис. 1.4, что граница области разгруженного материала имеет форму окружности, а тело имеет форму пластины единичной толщины, то высвобожденная энергия деформации, приходящаяся на единицу трещины, для плоского напряженного состояния равна половине произведения напряжения на относительную деформацию и на площадь релаксации.
Итак, количество энергии, расходуемой на образование новых поверхностей, пропорционально первой степени длины трещины, а количество высвобождаемой энергии пропорционально квадрату длины трещины. Следовательно, чем длиннее трещина, тем больше роль высвобождаемой энергии. Можно показать, что в рассматриваемой задаче Гриффитса, начиная с некоторой «критической» длины (зависящей от величины внешней нагрузки и свойств материала), трещина высвобождает больше энергии, чем потребляет. А так как тело всегда стремится уменьшить запасенную в нем энергию, то трещина длиной больше критической развивается стремительно и безостановочно, разрушая образец материала. Критическая (для заданных напряжений) длина трещины 21 будет соответствовать максимуму общей энергии тела W, равной поверхностной энергии, минус энергия, которая была высвобождена, чтобы трещина достигла длины 2l.
В нашем случае трещина заданной длины 2l при нагрузке меньше критической не распространяется. Если же нагрузка больше критической, то трещина развивается безостановочно, так как с увеличением длины трещины нагрузка, требуемая для ее продвижения, уменьшается (см. формулу 1.8), а фактически действующая нагрузка остатается неизменной. Такое развитие трещин называют неустойчивым. Возможно и устойчивое распространение трещин. Например, если вместо растяжения пластины равномерной нагрузкой а приложить в центре трещины к ее берегам две сосредоточенные растягивающие силы, то критическая величина этой силы
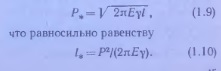
В этом случае после увеличения нагрузки выше критического значения трещина развивается постепенно, причем ее длина будет нарастать пропорционально квадрату величины нагрузки.
Дальнейшие этапы развития механики разрушения. Несмотря на то что теория Гриффитса была разработана применительно к очень хрупким и однородным материалам, впоследствии исследованиями Орована, Ирвина, Вестергаарда и других была показана возможность ее использования для более пластичных и неоднородных материалов, в частности для бетона. Эта возможность была основана на предположении, что высвобожденная энергия в значительной степени затрачивается на пластическое разрушение около вершины трещины (в местах резкой концентрации напряжений). Пластическое разрушение сопровождается значительной пластической деформацией; затрачиваемая при этом работа не зависит от начальной длины трещины и, следовательно, является такой же характеристикой сопротивления материала разрушению, как и поверхностная энергия при полностью упругом разрушении.
Введенную выше величину удельной плотности поверхностной энергии у можно рассматривать как состоящую из двух компонентов:
Для большинства технических материалов в процессе разрушения значительная часть затрачиваемой энергии расходуется на микропластические деформации. При этом отношение у/у0 может характеризовать степень хрупкости материала. Значения у, у0 и отношение этих величин для некоторых материалов (Дж/м2) приведены ниже.

Изложенный выше анализ развития трещин, берущий начало от Гриффитса, основан на энергетическом подходе, на законе сохранения и превращения энергии. Возможен и другой подход к анализу развития трещин, а именно силовой, когда рассматриваются условия равновесия действующих на трещину внешних сил (нагрузки) и внутренних сил (сил межчастичного сцепления).
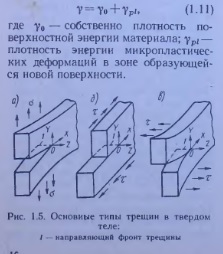
Силовой и энергетический подходы эквивалентны, т. е. они оба дают одинаковые результаты. Просто в ряде конкретных случаев применение того или иного подхода оказывается более удобным. Критерии локального разрушения материала около трещин. В силовом подходе детально рассматривают напряженное состояние у вершины (кончика) трещины — места возникновения наибольшей концентрации напряжений. Наиболее общий случай полей деформаций и напряжений у вершины можно получить путем комбинации трех частных видов деформаций. Вид I (рис. 1.5, а) связан с отрывом, когда края (поверхности) трещины расходятся в противоположных направлениях; вид II (рис. 1.5,6) соответствует поперечному сдвигу — перемещениям, при которых берега трещины скользят друг по другу параллельно плоскости, вид III (рис. 1.5, в) связан с антиплоской деформацией (разрезание ножницами), когда трещина находится в условиях продольного сдвига, причем края трещины скользят друг по другу параллельно направляющему фронту трещины 1.
Важнейшим моментом в механике разрушения является критерий локального разрушения, т. е. начала распространения трещины. Этот критерий не следует из уравнений равновесия или движения механики сплошных сред. Для формулировки критерия можно было бы вычислить напряжения у кончика трещины (с учетом их концентрации, см. рис. 1.3) и сравнить эти чрезвычайно высокие напряжения, например, с теоретической прочностью материала. Однако этот путь оказывается ненадежным: концентрация напряжений зависит в основном от реального радиуса кривизны трещины в ее кончике, а этот радиус, как правило, определить невозможно, во всяком случае, с требуемой степенью точности; да и сама величина теоретической прочности материала не поддается точному определению в опытах. Можно не учитывать реальный радиус кривизны трещины, считая этот кончик идеально острым («трещина — разрез»). Тогда концентрация напряжений становится такой сильной, что напряжения ау у кончика трещины, вычисляемые по методам теории упругости, будут стремиться к бесконечности, но по-разному в зависимости от формы трещины, формы тела и характера внешней нагрузки. Используем этот различный характер стремления напряжений cv к бесконечности для формулировки критерия локального разрушения тела.
Вернемся к формулировке критерия локального разрушения. Наиболее просто он формулируется в теории так называемых квазихрупких трещин, согласно которой наибольший размер области необратимых деформаций вблизи кончика трещины мал по сравнению с длиной трещины. Для наиболее распространенного (применительно к механике разрушения однородных материалов) случая трещин отрыва (вид 1-й см. рис. 1.5, а) этот критерий заключается в том, что коэффициент К1 при особенности (сингулярном члене) в формулах для напряжений вблизи кончика трещины в момент локального разрушения считается равным критическому коэффициенту интенсивности напряжений рассматриваемому как некоторая постоянная материала. Эта величина может быть выражена через модуль упругости Е, коэффициент Пуассона и эффективную плотность поверхностной энергии материала.
Изложенные выше решения основаны на некоторых упрощающих гипотезах; в частности, принята линейная связь между длиной трещины и энергией, расходуемой на образование новых поверхностей тела. Предполагается, что до достижения нагрузкой некоторого критического значения трещина абсолютно неподвижна. Решения, основанные на приведенных упрощающих гипотезах, образуют математический аппарат так называемой линейной механики разрушения.
Для более точного описания процесса развития трещин в бетоне предложены модели так называемой нелинейной механики разрушения.
Методы механики разрушения используются в бетоноведении, для моделирования на ЭВМ процесса деформирования и разрушения бетонов различной структуры (см. рис. 1.1.). Это позволяет путем числового эксперимента проследить влияние на деформативность и прочность бетона таких факторов, как количество и крупность заполнителя, форма его зерен, соотношение между модулями упругости и прочностными характеристиками заполнителя и цементного камня, прочностные и деформативные характеристики зоны контакта между заполнителем и цементным камнем и г. п. Проведение реального эксперимента с варьированием в достаточно широких пределах такого большого числа параметров весьма трудоемко; применение методов механики разрушения в сочетании с ЭВМ позволяет резко сократить сроки и трудоемкость подобных экспериментов. Методы механики разрушения, кроме того, начинают использоваться и непосредственно при расчетах строительных конструкций. В качестве примера можно привести методику расчета прочности строповочных деталей и отверстий (см. ниже § 7.8).
Контрольные вопросы 1. Как классифицируют бетон по объемной массе, по виду заполнителя, по зерновому составу заполнителей, по условиям твердения? 2. Каковы основные технические требования к бетону? 3. Каковы основные виды образцов для испытаний бетона на сжатие и растяжение? 4. Каковы основные классы бетона по прочности на сжатие и по прочности иа осевое растяжение? 5. Каковы основные марки бетона по морозостойкости, по водонепроницаемости, по средней плотности, по самонапряжению? 6. В зависимости от каких условий выбирают класс и марку бетона? 7. Что такое предел длительного сопротивления и предел выносливости бетона? Каковы их значения (в долях от временного сопротивления бетона)? 8. Какими величинами характеризуются деформативные свойства бетона при кратковременном нагружении? 9. Опишите свойства ползучести и усадки бетона. 10. Что такое концентрация напряжений и как она влияет иа рост трещин? 11. Что такое устойчивое и неустойчивое развитие трещин? 12. На каком законе природы основан энергетический подход к анализу развития трещин? 13. На каком принципе основан силовой подход к анализу развития трещин? 14. Как формулируется критерий локального разрушения (развития трещин) с использованием понятия критического коэффициента интенсивности напряжений?
