
Расчет прочности наклонных сечений по поперечной силе и изгибающему моменту
Изгибаемый железобетонный элемент может разрушиться не только по нормальному к оси балки сечению, но и по наклонному сечению, обычно расположенному вблизи опоры. Это связано с тем, что вблизи опор действуют не только изгибающие моменты, но и значительные поперечные силы, в соответствии с чем рассматривают два возможных случая разрушения по наклонному сечению — от изгибающего момента М и поперечной силы Q.
Построение условий прочности. При расчете прочности наклонных сечений исходят из условия, чтобы усилия от внешних нагрузок, действующие в наклонном сечении, были меньше или равны внутренним предельным усилиям в наклонном сечении. Усилия от внешних нагрузок представляют собой равнодействующую всех внешних сил (М и Q), расположенных по одну сторону от рассматриваемого наклонного сечения. Внутренние усилия в наклонном сечении определяются в предположении, что в этом сечении в предельном состоянии имеется наклонная трещина. Внутренние усилия в подобном наклонном сечении следующие: продольное и поперечное усилия в бетоне над наклонной трещиной; осевые и поперечные («нагельные») усилия в продольной арматуре, пересекающей наклонную трещину; осевые усилия в поперечной арматуре, пересекающей наклонную трещину; силы зацепления, действующие между берегами наклонной трещины. Рассмотрим природу этих внутренних усилий и какое они оказывают действие на сопротивление наклонного сечения внешним воздействиям.
Продольные и поперечные усилия в бетоне над наклонной трещиной представляют собой равнодействующие нормальных и касательных напряжений в нормальном сечении, проходящем через вершину наклонной трещины. Бетон в этой зоне работает в условиях сложного (неодноосного) напряженного состояния.
Продольная арматура, пересекающая наклонную трещину, в результате взаимного смещения берегов трещины удлиняется и изгибается. За счет этого в продольной арматуре возникают продольные усилия, моменты и поперечные усилия, определяемые соответственно осевыми напряжениями в арматуре, разностью краевых напряжений и приращением моментов по длине арматурного стержня. Однако напряжения в продольной арматуре к моменту разрушения сечения, как правило, не достигают своих предельных значений и не могут быть выражены через расчетные сопротивления арматуры.
Напряжения в большинстве стержней поперечной арматуры, пересекающей наклонную трещину, напротив, достигают предельных значений, т. е. расчетных сопротивлений. Поскольку в этих стержнях достигается предел текучести по всей площади стержня, то в арматуре действуют лишь осевые усилия, а поперечные («нагельные») являются весьма незначительными.
Силы зацепления, действующие между берегами наклонной трещины, являются следствием взаимного смещения этих берегов. Дело в том, что наклонные трещины имеют, как правило, ломаную конфигурацию, а сама поверхность бетона в трещине является шероховатой. Поэтому при смещении соответствующих точек берегов наклонной трещины возникают силы зацепления впадин и выступов. Силы зацепления могут играть большую роль в работе сечения, особенно при отсутствии поперечной арматуры.
В процессе постепенного увеличения внешней нагрузки вначале образуется наклонная трещина. После этого при дальнейшем росте нагрузки напряжения в обоих видах арматуры (продольная и поперечная) и в бетоне над наклонной трещиной непрерывно увеличиваются. Расчетное сопротивление вначале достигается напряжениями в поперечной арматуре, а затем, в процессе текучести, наступает также предельное состояние либо бетона над наклонной трещиной, либо продольной арматуры. В первом случае разрушение бетона вызовет разрушение элемента в целом, хотя напряжения в продольной арматуре и не достигли предельных значений. Во втором случае нагрузка может расти и далее, пока не разрушится бетон над трещиной или не нарушится анкеровка продольной арматуры, находящейся под предельными напряжениями. Возможен и третий вариант разрушения — при значительном насыщении элемента поперечной арматурой она не может достичь своих предельных сопротивлений и элемент разрушается от раздавливания бетона в середине высоты элемента, между наклонными трещинами.
В принципе расчет должен обеспечивать конструкцию от всех перечисленных случаев разрушения, причем для решения этой задачи можно использовать систему трех уравнений равновесия в наклонном сечении - равновесия поперечных сил, равновесия моментов, равновесия продольных сил. Однако методика, основанная на совместном решении всех уравнений равновесия, в настоящее время только разрабатывается, поэтому в нормах принимается раздельный расчет на действие поперечной силы и на действие момента в наклонном сечении.
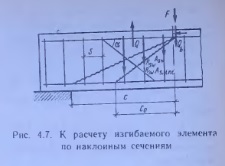
При первом типе разрушения по поперечной силе условие прочности наклонного сечения формулируется на основе следующих предпосылок (рис. 4.7): а) поперечное усилие, воспринимаемое бетоном над наклонной трещиной, вычисляется в зависимости от расчетного сопротивления бетона растяжению, размеров элемента и наклона сечения; б) усилия в поперечной арматуре всегда направлены вдоль стержней; в) в расчет вводится вся пересекаемая наклонным сечением поперечная арматура с растягивающими напряжениями. Под поперечной арматурой в этом случае понимают как отогнутые стержни, так и хомуты (поперечные стержни сварных каркасов или хомуты вязаных каркасов).
Условие прочности при первом типе разрушения - по поперечной силе:

Это условие вытекает из уравнения проекций усилий.
При втором типе разрушения — по изгибающему моменту условие прочности наклонного сечения основано на том, что сумма моментов относительно точки приложения равнодействующей сжимающих усилий в сечении над трещиной должна быть равна нулю:

Расчет прочности наклонных сечений по поперечной силе при поперечной арматуре в виде хомутов (без отгибов). Перед тем, как приступить к расчету по поперечной силе, необходимо проверить условие для предельного значения поперечной силы. Это необходимо, чтобы избежать раздавливания бетона по сжатой полосе между наклонными трещинами от действующих наклонных сжимающих усилий.
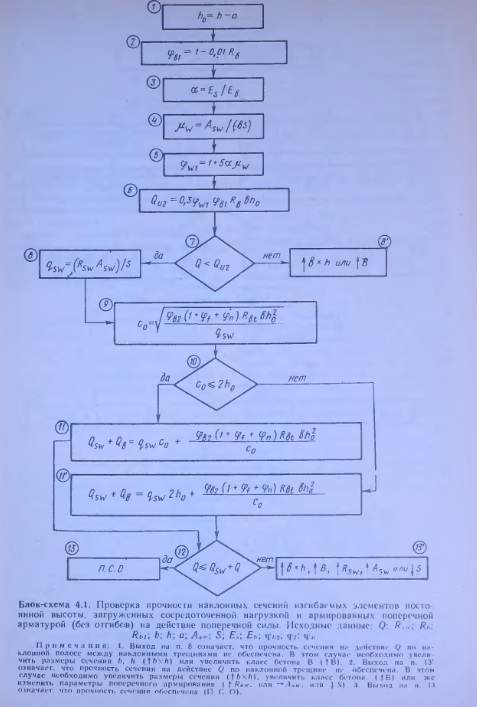
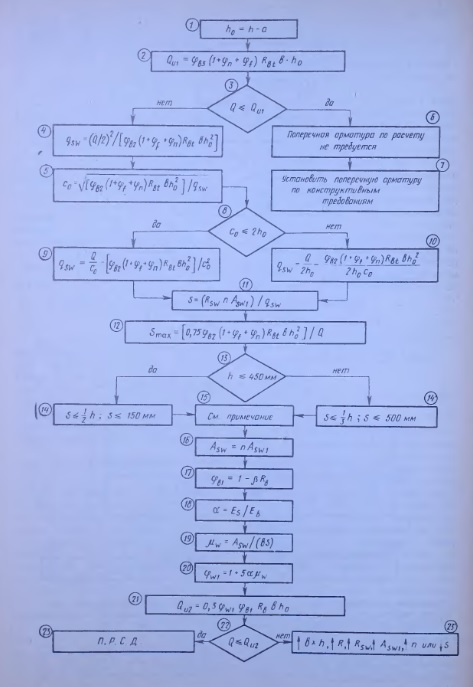
Для того чтобы яснее представить себе последовательность отдельных этапов расчета и их логическую взаимосвязь, можно воспользоваться приводимыми ниже блок-схемами расчета (блок-схемы 4.1 и 4.2). Эти же блок-схемы могут быть использованы для составления программ расчета на ЭВМ. Блок-схемы включают в себя арифметические и логические этапы расчета. Арифметические этапы заключаются в проведении вычислений по определенным формулам; они представлены в виде прямоугольников. Логические этапы предусматривают проверку выполнения определенных условий и (в зависимости от того, выполняется условие или нет) переход от предыдущего арифметического этапа к одному из последующих; логические этапы представлены на блок-схеме ромбами. Выполнение операций производится в направлении, указанном стрелками. Порядок вычислений по блок-схеме 4.2 приводится в примере 4.6.
Расчет наклонных сечений при комбинированном поперечном армировании (отгибы и хомуты). При армировании балок каркасами отогнутые стержни (отгибы) применяют сравнительно редко. Условие прочности элемента при комбинированном поперечном армировании было дано выше (формула 4.37):

Таким образом, отгибы воспринимают избыток поперечной силы Q. Расчет по поперечной силе следует производить для наклонных сечений, проходящих через следующие точки: 1 — грань опоры, 2 — начало расположенных в растянутой зоне отгибов; 3 точка изменения шага хомутов (рис. 4.8). В соответствии с этим величина Q в формуле (4.49) равна, для первой от опоры плоскости отгибов — поперечной силе Q у грани опоры; для второй от опоры плоскости отгибов — значению поперечной силы Q у нижней точки первой плоскости отгибов и т.д.
Конструктивные требования при армировании изгибаемых элементов отгибами и хомутами заключаются в следующем. Отгибы стержней осуществляют по дуге радиуса не менее 10 d, а на концах отогнутых стержней следует устраивать прямые участки, принимаемые не менее 20 d в растянутой и 10 d в сжатой зоне. Начало отгиба в растянутой зоне должно отстоять от нормального сечения, в котором отгибаемый стержень используется по расчету, не менее чем на 0,5 h0, а конец отгиба должен быть расположен не ближе того нормального сечения, в котором отгиб не требуется по расчету. Все приведенные выше формулы справедливы для расчета как прямоугольных, так и тавровых сечений.
Элементы без поперечной арматуры. Поперечная арматура, согласно требованиям норм, должна устанавливаться в балках и ребрах высотой более 150 мм и в многопустотных панелях перекрытий (или аналогичных часторебристых конструкциях) высотой более 300 мм. При меньшей высоте в указанных конструкциях, а также в сплошных плитах поперечную арматуру можно не устанавливать. При этом требуется проводить расчет таких элементов на действие поперечной силы. Расчет элементов без поперечной арматуры на действие поперечных сил имеет определенные особенности, связанные с условиями образования и развития наклонных трещин в таких элементах. В процессе увеличения нагрузки в них вначале появляются трещины в нормальных сечениях, расположенных в зоне максимального момента, после чего образуются нормальные трещины и в зоне поперечных сил. Эти трещины постепенно слегка отклоняются от своего направления в сторону траектории главных сжимающих напряжений. Наконец, возникает самостоятельная наклонная трещина (иногда она образуется из нормальной). По этой наклонной («критической») трещине и происходит разрушение, которое может наступить или сразу, или же после некоторого дополнительного увеличения нагрузки.
Эксперименты показали, что принятый в нормах расчет наклонных сечений на поперечную силу не учитывает ряда важных факторов. В частности, на несущую способность наклонного сечения, оцениваемую по предельной поперечной силе, оказывает влияние действующий в этом же сечении изгибающий момент, приводящий к увеличению напряжений в бетоне и арматуре. Поэтому с ростом изгибающего момента предельная поперечная сила должна уменьшаться. Этот учет, по-видимому, будет сделан за счет совместного решения уравнений равновесия поперечных сил и изгибающих моментов в наклонном сечении.
Расчет прочности наклонных сечений на действие изгибающего момента. Общее условие прочности наклонного сечения по изгибающему моменту записывают в виде формулы (4.38). Оказывается, что при определенных конструктивных условиях, перечисленных далее, прочность наклонного сечения будет по крайней мере не ниже, чем прочность нормального сечения этой же балки, и расчет наклонного сечения на изгибающий момент можно не производить.
Конструктивные требования, обеспечивающие прочность балки на изгиб по наклонным сечениям, следующие:
1) при свободном опирании балки должна быть обеспечена анкеровка продольных стержней, доводимых до опоры; в этом случае условие прочности элемента на изгиб гарантируется не только в пролете, но и во всех наклонных сечениях, начинающихся у опоры;
2) для обеспечения анкеровки арматуры периодического профиля длина ее запуска за грань свободной опоры должна составлять
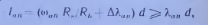
3) если анкеровка продольных стержней недостаточна, то предусматривают специальные конструктивные меры — приварку к концам стержней анкеруюших пластин или закладных деталей, постановку косвенной арматуры в зоне анкеровки и т. п.
В целях экономии стали часть продольной арматуры (не более 50 %) можно обрывать в пролете, не доведя до опоры. Обрываемые стержни должны быть заведены за место теоретического обрыва (т. е. за нормальное сечение, где они уже не требуются по расчету) на длину, принимаемую равной большему из двух значений:

Контрольные вопросы. 1. Что такое плиты и балки? 2. Для чего служит продольная и поперечная арматура в балках? 3. Как размещаются сетки в плитах? 4. Какие конструкции называют предварительно напряженными (преднапряженными)? 5. Каковы основные преимущества преднапряженных конструкций? 6. Каковы два основных способа создания предварительных напряжений в арматуре и в чем их особенность? 7. Какие классы арматуры и классы бетона применяют для предварительно напряженных конструкций? 8. Что такое передаточная прочность бетона? 9. Как обеспечивается усиление концевых участков предварительно напряженных элементов? 10. Какие виды анкерных устройств
